|
Discussion rcortesi Saturday, 13 Dec 03 1:57 am EST
|
|
Ideal Gas
Adiobatic Bounary
Quasi-Static Compression
Initial Pressure in the cylinder is atmospheric pressure
Solve For:
Force as a function of displacement.
Here is a simple drawing of the piston
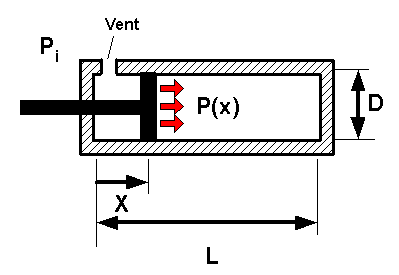
|
|
Discussion rcortesi Saturday, 13 Dec 03 4:53 pm EST
|
|
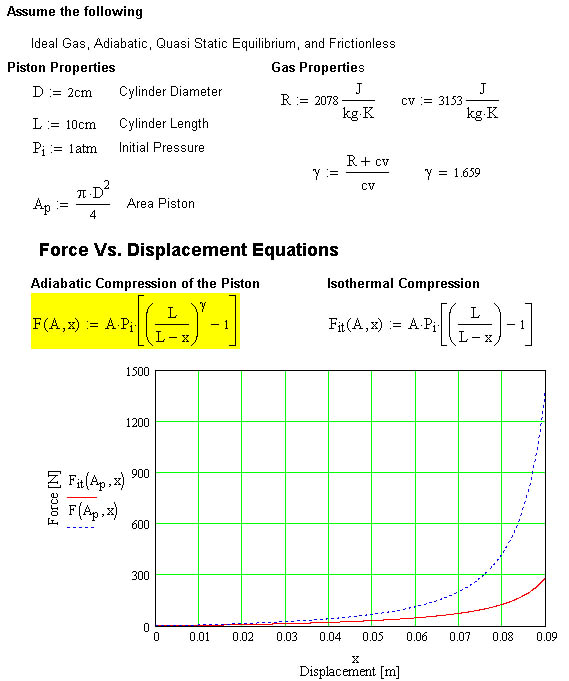
This plot compares the compression of an isothermal and adiabatic piston.
The isothermal compression would only be true if the piston were compressed slow enough that the gas could come into equilibrium with its surroundings. This is not typical for the systems we are talking about.
We can see that the adiabatic compression (i.e. no heat transfer through the cylinder walls) results in a steeper Force Displacement Curve (blue) than the slower isothermal case (red).
Length: 0.10 m
Diameter: 0.02 m
Atmospheric Pressure: 1 atm
Dispacement from 0 to 0.09 m
|
|
|
Discussion rcortesi Thursday, 12 Feb 04 3:59 am EST
|
|
Lets say you compress a piston. The force you would have to apply would be determined by the adiabatic function above (gamma = 1.6).
You then left the piston compressed over night. The temperature in the piston equalized with its suroundings (it cools). In the moring you find the piston is pushing with less force and less engery is stored. The amount of force that it was pushing with and energy stored is more closely approximated by the isothermal case (gamma = 1).
|
|
|
Discussion rcortesi Saturday, 13 Dec 03 4:59 pm EST
|
|
The force vs. displacement relationship plotted above was for a particular sized piston. You can see the relationship between meters of displacement and Newtons of force.
What if I want force in units of lbs, or displacement in inches, or a different sized piston?
The Force Factor
Notice that the force function is directly proportional to piston area, and initial pressure (assume to be atmospheric pressure in this analysis). So, if I double the area of the piston I double the force.
I can analysis everything in dimensionless number the results can be easily applied to any size piston in any unit set. Piston displacement is measured in % of sealed length, and force is measured as a factor of the initial force, I call this the force factor. Initial force equals initial pressure multiplied by piston area.
Force Factor = Foce Out / (Piston Area * Atmospheric Pressure)
Example 1
|
What force (in lbs) is required to expand a 2cm diameter piston (area = 0.487 in^2) with an initial sealed length (L) of 10 cm, by 2 cm (x)?
Use an initial pressure of 14.7 psi (1 atm). Multiplying initial pressure by area gives an initial force of 7.16 lbs. Expanding the piston by two cm is a 20% expansion.
Looking at the force vs displacement expansion plot, gives a force factor is about 0.25.
Then multiply the initial force by 0.25 and you find it would take about 1.8 lbs to compress the piston this much.
|
The % Displacement
Displacement is measure in percent of sealed length.
% Displacement = x/L
Of course if you are doing lots of analysis with a particular sized pisiton in a particlar unit set you can calulate it out from displacement to force using the equations (watch out for units!!!).
|
|
Discussion rcortesi Monday, 12 Jan 04 1:06 pm EST
|
|
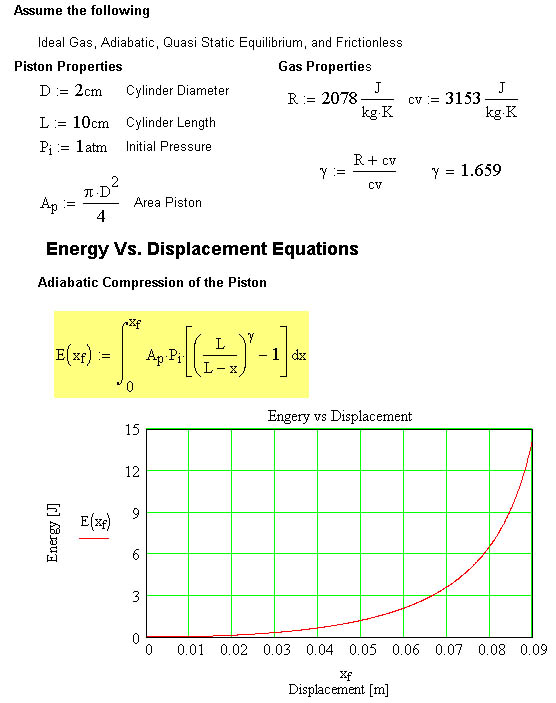
Here is a plot of energy vs displacement for a 2.007 sized piston.
|
|
Discussion rcortesi Saturday, 31 Jan 04 12:00 am EST
|
|
The force vs. displacement equation allows us to treat the pison as a non-linear spring. Further more we can adjust the "spring constant" of the piston by changing the inital sealed length (L). Make L smaller and the piston becomes stiffer for a given displacement.
Example 2
|
Determine the what the initial sealed length (L) should be (in cm) for a 3cm diameter piston to require 200 N force for a 1 cm displacement?
Calculate the initial force by:
piston area (0.0007 m^2) * Initial Pressure (1 atm = 101300 Pa) = 72 N.
Find the force factor for the desired output force:
200 N / 72N = a force factor of 2.8.
Looking at the force vs displacement compression plot we see that this corispons to a % displacement of 55%.
So to find the intial seal length L
x (1 cm) / % displacement (55%) = L (1.8 cm)
|
|
|
Discussion rcortesi Thursday, 12 Feb 04 2:50 am EST
|
|
Does it matter if we pull on the piston or push on it?
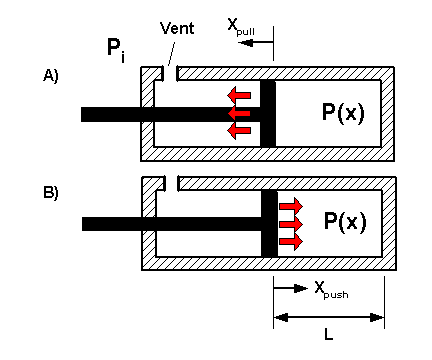
The figure above shows two pistons. Both are vented on the left side (connecting rod side), and sealed on the right side. Both start with the SAME sealed volume. The top piston (a) is pulled, so the sealed volume is expanded. The bottom piston (b) is pushed so the sealed volume is compressed.
The plot below shows the results. X is the percent displacement of the original sealed volume (or piston length). The force factor is described above.
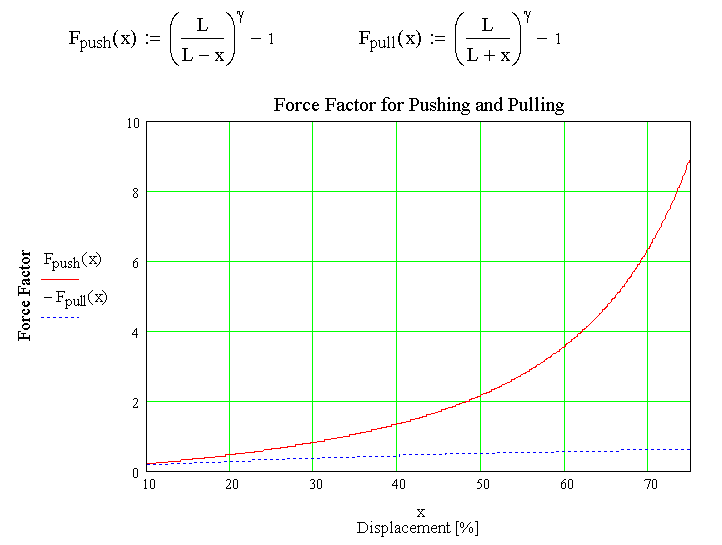
From the plot above we can see that pushing (red) and pulling (blue) behave very differently.
Surprised? Think of it this way, the force exerted by the piston proportional to the pressure difference across the pistong. The only limit on how high a pressure difference in the pushing case is how hard you can push and when the piston will rupture. In the pulling case even if you could pull the piston far enough to get a perfect vacuum (which you can't) the largest pressure difference across the piston would be bewteen atmospheric pressure and the vacuum.
|
|
|
Discussion rcortesi Thursday, 12 Feb 04 3:29 am EST
|
|
In the compression case the displacement could not exceed 100%, because that is end the piston has commpressed the volume to 0 (in fact it should be obvious that you can't even get to 100% with out a leak). But this is not a limit for the expansion case.
The plot below shows the force factor as a function of displacement from 0 to 500% of the origenal sealed length.
We can see that the force factor approaches 1 (i.e. atmospheric pressure * piston area = force).
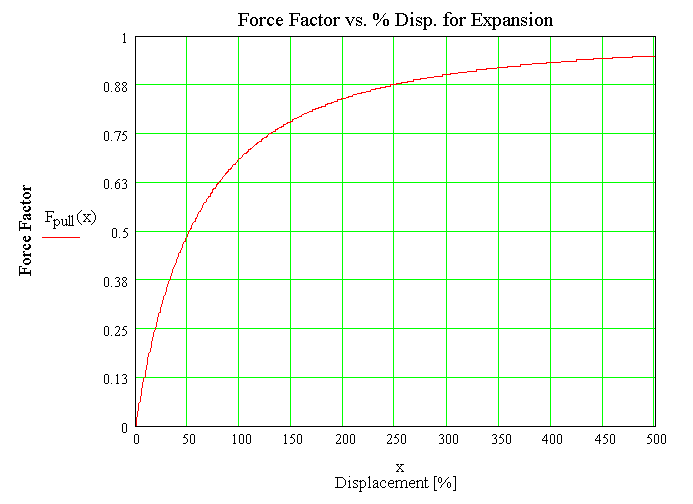
We can also see from this plot that change in force becomes mush less for given displacement after about 200%. This means that the spring would become "softer".
|
|
|
Discussion rcortesi Thursday, 12 Feb 04 2:55 am EST
|
|
We can see that initial pressure is one of factors in force and energy equations. This makes sence becuase because the higher the initial pressure the more air molicules have to be compressed, conversely if the piston was in a vacuum inside and out then there would be no spring like effect.
So how much does initial pressure matter? Would a low pressure area moving through change performace significantly, what about operating in Denver, or on Everest?
NoteThis assumes that the initial atmospheric pressure what is sealed in the pison.
Let's try some different values for intial pressure to see how big an effect it has.
We should note that for a given x, L, and D force varies linearly with initial pressure. An extreme weather shift would cause a change in atmospheric pressure of about 60 hPa. This would be like going from an eye of a huricane (960 kPa) to a very high pressure zone (1020 hPa). 1 atm is 1013 hPa. So 60/1013 = 6%. So if you machine went from one extreme weather extreme to the other then you could expect the amount of force and stored energy to change by 6%.
If your machine was on everest where atmospheric pressure is around 300 hPa then you would only have 1/3 the available energy.
|
|
Discussion rcortesi Thursday, 12 Feb 04 2:59 am EST
|
|
A simple spring has the form F = K * x.
If the gas spring is not compressed or expanded too much then it can be modeled as a linear process.
A good way of figuring out how much compression is too much is to look at the plots of the non-linear force vs. displacements.
|
|
|
Discussion rcortesi Thursday, 12 Feb 04 3:05 am EST
|
|
The plot below shows force factor vs displacement for a piston being compressed from 0 to 60%. A bit fit line is drawning to approximate the force vs. displacement relationship linearly.
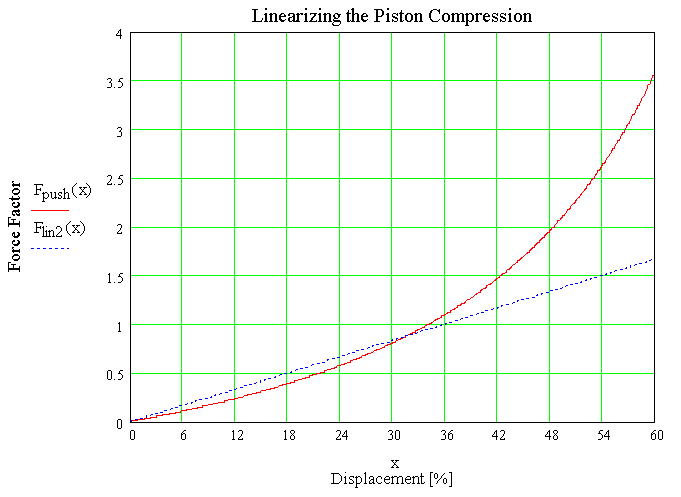
We can see that a linear "spring constant" of 0.028 give a good linear model up to about 40% displacement.
The spring constant is relating the force factor (dimensionless) to % displacement. So to get a force value as a function of displacement you would have to use
F = A * Patm * K * disp/L.
|
|
Discussion rcortesi Thursday, 12 Feb 04 3:18 am EST
|
|
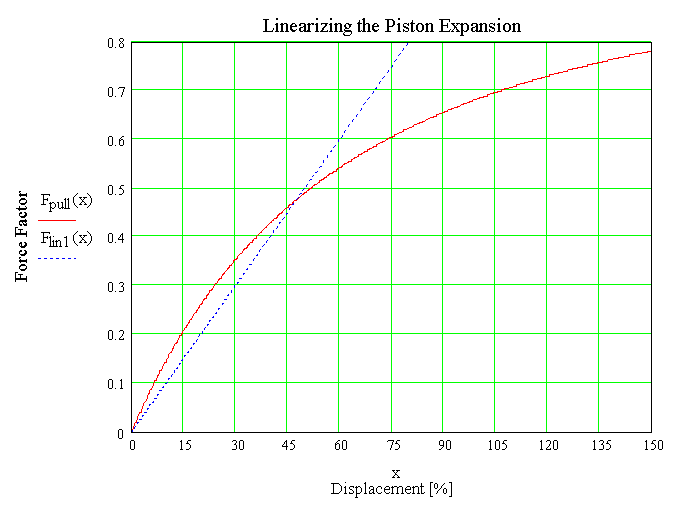
In the expansion case a linear "spring constant" of 0.01 is a good linear approximation of the process up to about 60% displacement, as show by the plot below.
|
|
|
Discussion rcortesi Thursday, 12 Feb 04 12:26 pm EST
|
|
|
|







